| المجموعات الإجتماعية |
| البحث |
| مشاركات اليوم |
 |
| دروس تقنية وصيانة الطائرات يقديم شروح لمنظومات الطائرة تعرض على شكل دروس بطريقة اكاديمية مبسطة |
| إضافة رد |
|
|
أدوات الموضوع |
 |
| دروس تقنية وصيانة الطائرات يقديم شروح لمنظومات الطائرة تعرض على شكل دروس بطريقة اكاديمية مبسطة |
| إضافة رد |
|
|
أدوات الموضوع |
| مشاركة [ 1 ] | ||||
|
||||
|
|
 Basic Definitions speed of sound The speed of sound is a basic property of the atmosphere that changes with temperature. For a given set of conditions, the speed of sound defines the velocity at which sound waves travel through a substance, such as air. Scientists have devised a standard atmosphere model that defines typical values for the speed of sound that change with altitude. Mach number Mach number is a quantity that defines how quickly a vehicle travels with respect to the speed of sound. The Mach number (M) is simply the ratio of the vehicle's velocity (V) divided by the speed of sound at that altitude (a). 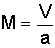 For example, an aircraft flying at Mach 0.8 is traveling at 80% of the speed of sound while a missile cruising at Mach 3 is traveling at three times the speed of sound. subsonic A vehicle that is traveling slower than the speed of sound (M<1) is said to be flying at subsonic speeds. supersonic A vehicle that is traveling faster than the speed of sound (M>1) is said to be flying at supersonic speeds. sound barrier The term sound barrier is often associated with supersonic flight. In particular, "breaking the sound barrier" is the process of accelerating through Mach 1 and going from subsonic to supersonic speeds. The term originated in the 1940s when researchers discovered a large increase in drag that seemed to indicate that an infinite amount of thrust would be needed to fly at the speed of sound. In other words, some believed that a physical barrier existed that would prevent an aircraft from ever being able to travel at supersonic speeds. Since there obviously is no such barrier, the term sound barrier is outdated and really should not be used any more. Nevertheless, it has become a popular part of human speech, and continues in use. Calculating the Speed of Sound As indicated above, the speed of sound is not a single value, but changes with altitude. To be more precise, the speed of sound (a) can be directly calculated based on the air temperature (T), and temperature is a function of altitude. A procedure for calculating the temperature, as well as the density and pressure, using the standard atmosphere model was described in a previous question. Towards the end of that explanation, an equation for calculating the speed of sound based on temperature is also introduced. This equation is based on the more general form . 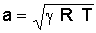 where a = speed of sound [ft/s or m/s] g = specific heat ratio, which is usually equal to 1.4 R = specific gas constant, which equals 1716 ft-lb/slug/°R in English units and 287 J/kg/K in Metric units T = atmospheric temperature in degrees Rankine (°R) in English units and degrees Kelvin (K) in Metric units Once the speed of sound is known, the Mach number can be easily computed by dividing the airspeed of the vehicle by the speed of sound. Or conversely, the airspeed of the vehicle can be found by multiplying the speed of sound by the Mach number. Here at Aerospaceweb.org, we've provided an atmospheric properties calculator to simplify these calculations. The user simply enters an altitude and the calculator will provide the air temperature and speed of sound at that altitude. The user can also enter a velocity or a Mach number at that altitude and the calculator will compute the corresponding airspeeds. However, it should be noted that the above methodology is based on the standard atmospheric model, which assumes a temperature at sea level of 60°F (15°C). For most engineering purposes, this model is sufficiently accurate for computing the speed of sound, and the change in speed due to a different temperature is small enough that it can be neglected. However, if one already knows the temperature at a given altitude and wishes to calculate a more precise value for the speed of sound, the following equations can also be used. The first is specific to English units while the second applies to the Metric System. 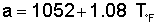 where a = speed of sound [ft/s] T°F = atmospheric temperature in degrees Fahrenheit (°F) 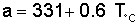 where a = speed of sound [m/s] T°C = atmospheric temperature in degrees Celsius According to these equations, a 1°F change in temperature produces a 1.08 ft/s change in the speed of sound, or a 1°C change causes a 0.6 m/s change in the speed of sound. This difference is insignificant enough that we can usually ignore it and use the standard atmospheric model as is. Values of the Speed of Sound One of the most common questions we receive is fow fast is the speed of sound, and as was pointed out earlier, there is no single value to quote. The speed of sound, also known as Mach 1, changes throughout the atmosphere based on the temperature at any given altitude. Probably the most important value to remember, however, is the speed of sound at sea level. Based on the standard atmospheric model, this value has been defined to be
If you were to reach Mach 1, or "break the sound barrier," at sea level, the above speed is how fast you would have to travel in order to do so. Another question we often receive is how fast is the speed of sound at other altitudes besides sea level. While the most accurate method of computing these values would be to use the equations listed above or an atmospheric properties calculator, we realize that this method is not always the most convenient approach. In light of this fact, we have provided tables listing the speed of sound in both English and Metric units for altitudes ranging from below sea level to the edge of the atmosphere. These tables provide the accepted values for Mach 1 in small increments of altitude allowing the reader to observe how the speed of sound varies through different regions of the atmosphere. Mach Number Examples A final question that comes up frequently is how fast is Mach 2, 3, 5, 10, or any other value besides Mach 1 at a given altitude. We first addressed this topic in a question regarding how fast is Mach 2 in miles per hour. Here, we pointed out that the Mach number is a multiple of the speed of sound. Therefore, if you know the value of Mach 1 in miles per hour, feet per second, kilometers per hour, or any other unit of measurement at the altitude in question, you merely have to multiply that value by the desired Mach number to determine the speed in that particular unit. For example, say we wanted to know the speed of a cruise missile traveling Mach 0.8 at sea level in knots. To solve the problem, we can use the speed of sound value listed above at sea level, given as 661.5 knots, and multiply it by 0.8. The answer turns out to be 529 knots. Yet another example is provided above when someone asks, "what is the speed of an aircraft traveling at Mach 3 at an altitude of 30,000 feet?" If we take another look at the Mach 1 vs. altitude tables already discussed, we see that the speed of sound at 30,000 ft is 678.2 miles per hour. All we have to do is multiply this value by 3 to determine the speed of a vehicle traveling Mach 3 at 30,000 ft in miles per hour. The answer is 2,035 mph. Let us now consider an example of the opposite problem. About 8 1/2 minutes into the flight of a Space Shuttle, the vehicle's main engines are disengaged. At that point in its trajectory, the Shuttle is traveling about 7,000 meters per second at an altitude of 110,000 m. What is the Shuttle's Mach number? If we again look at the Mach 1 vs. altitude tables, we see that the |
|||
|
|

|
| مشاركة [ 2 ] | ||||
|
||||
|
|
موضوع مشوق
شكرا علي الموضوع |
|||
|
|

|
| مشاركة [ 3 ] | ||||
|
||||
|
|
شكرا لك أخي
على موضوعك وما قدم من معلومات |
|||
|
|

|
| مشاركة [ 4 ] | ||||
|
||||
|
|
لكن اخي الكريم ياريت تكمل باقي الموضوع فيما يخص جدول علاقة الارتفاع و الماخ نمبر
ولك كامل الشكر
5A-ALI |
|||
|
|

|
| مشاركة [ 5 ] | ||||
|
||||
|
|
حياك الله اخي العزيز كابتن طارق
جهود تستحق الشكر الجزيل وياليت يعزز الموضوع ببعض الصور التوضيحية بارك الله فيك تفبل تحياتي |
|||
|
|

|
| مشاركة [ 6 ] | ||||
|
||||
|
|
[QUOTE=5A-ALI;588746]لكن اخي الكريم ياريت تكمل باقي الموضوع فيما يخص جدول علاقة الارتفاع و الماخ نمبر
ولك كامل الشكر 5A-ALI حاضرين أخي الكريم لك بعض الجداول التي تبين العلاقة بين الأرتفاع والماخ The first table is in the English System and indicates the speed of sound in miles per hour (mph), feet per second (ft/s), and knots (kts) for altitudes from -15,000 ft to 400,000 ft in 5,000 ft increments . 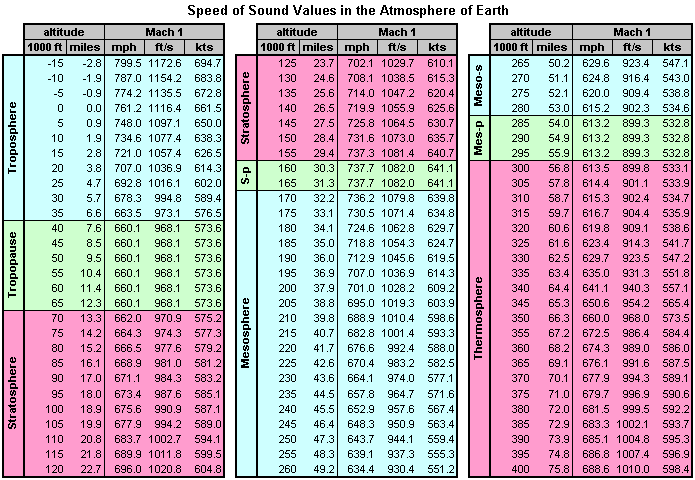 The tables are also color-coded to correspond to different regions of the atmosphere. These regions are defined by the behavior of the atmospheric temperature and (by extension) the speed of sound as altitude increases. These regions include : 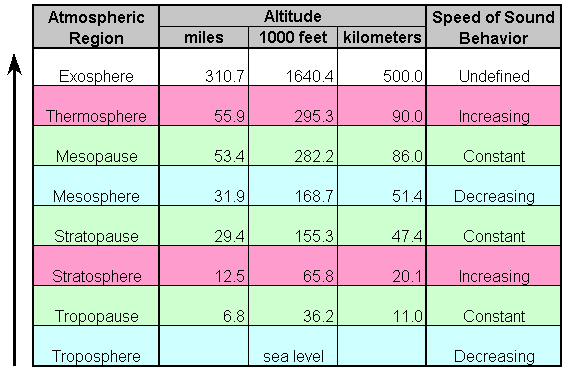 The Mach 1 tables are .gif image files that you can download or print for future reference. Furthermore, the tables can be used to determine the speeds associated with multiples of Mach 1. Mach number (M) is a ratio comparing the velocity of a vehicle (V) against the speed of sound (a):
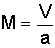 Knowing M and a, we can also rearrange the above equation to the following form to solve for the velocity V : 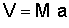 If you want to know a multiple of the speed of sound at any particular altitude, simply multiply the value of Mach 1 at the altitude of choice by the desired Mach number. For example, Mach 5 at sea level is 5 times the value of Mach 1 at an altitude of 0 ft (0 m): Mach 5(SL) = 5 * (761.2 mph) = 3806 mph Mach 5(SL) = 5 * (1116.4 ft/s) = 5582 ft/s Mach 5(SL) = 5 * (340.3 m/s) = 1701.5 m/s Mach 5(SL) = 5 * (1225 km/h) = 6,125 km/h Mach 5(SL) = 5 * (661 kts) = 3305 kts These tables were created using the 1976 US Standard Atmosphere. Unfortunately, most textbooks and computer programs that provide Standard Atmosphere tables only go up to a height between 200,000 and 295,000 ft (61 to 90 km). Sources that do provide speed of sound values beyond these altitudes are rather contradictory. To extend our tables up to 400,000 ft (122 km), a few known data points were used to linearly interpolate the remaining values. While the Mach 1 values provided for the Thermosphere may not be precise, they should be reasonable approximations. Beyond 400,000 ft (122 km), the air density is so low that the atmosphere essentially ceases to exist and the speed of sound becomes undefined. It is for these reasons that is considered to be about 400,000 ft, or 76 miles (122 km). الرابط التالي أخي الكريم بة أتوماسفيرك كالكوليتر لحساب الكثير من الأشياء مثل الماخ . والأرتفاع . والسرعة . والضغط . ودرجة الحرارة . والكثافة . والعجلة .وأشياء كثرة مفيدة أتمني أن تنال أعجابكم |
|||
|
|

|
| مشاركة [ 7 ] | ||||
|
||||
|
|
مشكور وبارك الله فيك علي الموقع الجميل هذا من زمان وانا دايخ علي هالموقع وتستحق التقييم
  |
|||
|
|

|
| مشاركة [ 8 ] | ||||
|
||||
|
|
موقع جميل جدا
يمكن ان تحمل منه برنامج AtmosCalculator الله يعطيك االعافية علي هالموقع و اذا كان عندك مواقع غيره لا تحرمنا منها |
|||
|
|

|
| مشاركة [ 9 ] | ||||
|
||||
|
|
[QUOTE=5A-ALI;588734]موضوع مشوق
شكرا علي الموضع مشكور أخي الكريم علي المرور والتعقيب [QUOTE=libyan-ame;588737]شكرا لك أخي على موضوعك وما قدم من معلومات أخي الكريم libyan-ame شكراً لك علي المرور والتعقيب خالص ودي لك [QUOTE=عماد المشهداني;589098] حياك الله اخي العزيز كابتن طارق جهود تستحق الشكر الجزيل وياليت يعزز الموضوع ببعض الصور التوضيحية بارك الله فيك تفبل تحياتي حياك الله أخي عماد شكراً لك علي مرورك وتعقيبك مع ودي [QUOTE=5A-ALI;589345]موقع جميل جدا يمكن ان تحمل منه برنامج AtmosCalculator الله يعطيك االعافية علي هالموقع و اذا كان عندك مواقع غيره لا تحرمنا منها أخي 5A-ALi شكراً لك علي المرور
وتاكد أنو آي موقع مفيد لن أبخل به عليكم تقبل خالص ودي لك |
|||
|
|

|
| مشاركة [ 10 ] | ||||
|
||||
|
|
مجهود يستحق الشكر والتقدير
تقبل مروري |
|||
|
|

|
| مشاركة [ 11 ] | ||||
|
||||
|
|
السلام عليكم ورحمة الله وركاته
الموهبين في الدنيا وبذات العرب كثرين وخصوصآ المسلمين عن خمس عقول من الغرب والحمدالله في منهم اخوي شكر ع الموظوع بس ياليت يكون في شرح بلعربي لأني للاسف لااجيد الانقليزي ومن محبين البداع في الطائرات تحياتي للجميع |
|||
|
|

|
| مشاركة [ 12 ] | ||||
|
||||
|
|
 Basic Definitions speed of sound The speed of sound is a basic property of the atmosphere that changes with temperature. For a given set of conditions, the speed of sound defines the velocity at which sound waves travel through a substance, such as air. Scientists have devised a standard atmosphere model that defines typical values for the speed of sound that change with altitude. Mach number Mach number is a quantity that defines how quickly a vehicle travels with respect to the speed of sound. The Mach number (M) is simply the ratio of the vehicle's velocity (V) divided by the speed of sound at that altitude (a). 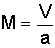 For example, an aircraft flying at Mach 0.8 is traveling at 80% of the speed of sound while a missile cruising at Mach 3 is traveling at three times the speed of sound. subsonic A vehicle that is traveling slower than the speed of sound (M<1) is said to be flying at subsonic speeds. supersonic A vehicle that is traveling faster than the speed of sound (M>1) is said to be flying at supersonic speeds. sound barrier The term sound barrier is often associated with supersonic flight. In particular, "breaking the sound barrier" is the process of accelerating through Mach 1 and going from subsonic to supersonic speeds. The term originated in the 1940s when researchers discovered a large increase in drag that seemed to indicate that an infinite amount of thrust would be needed to fly at the speed of sound. In other words, some believed that a physical barrier existed that would prevent an aircraft from ever being able to travel at supersonic speeds. Since there obviously is no such barrier, the term sound barrier is outdated and really should not be used any more. Nevertheless, it has become a popular part of human speech, and continues in use. Calculating the Speed of Sound As indicated above, the speed of sound is not a single value, but changes with altitude. To be more precise, the speed of sound (a) can be directly calculated based on the air temperature (T), and temperature is a function of altitude. A procedure for calculating the temperature, as well as the density and pressure, using the standard atmosphere model was described in a previous question. Towards the end of that explanation, an equation for calculating the speed of sound based on temperature is also introduced. This equation is based on the more general form . 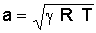 where a = speed of sound [ft/s or m/s] g = specific heat ratio, which is usually equal to 1.4 R = specific gas constant, which equals 1716 ft-lb/slug/°R in English units and 287 J/kg/K in Metric units T = atmospheric temperature in degrees Rankine (°R) in English units and degrees Kelvin (K) in Metric units Once the speed of sound is known, the Mach number can be easily computed by dividing the airspeed of the vehicle by the speed of sound. Or conversely, the airspeed of the vehicle can be found by multiplying the speed of sound by the Mach number. Here at Aerospaceweb.org, we've provided an atmospheric properties calculator to simplify these calculations. The user simply enters an altitude and the calculator will provide the air temperature and speed of sound at that altitude. The user can also enter a velocity or a Mach number at that altitude and the calculator will compute the corresponding airspeeds. However, it should be noted that the above methodology is based on the standard atmospheric model, which assumes a temperature at sea level of 60°F (15°C). For most engineering purposes, this model is sufficiently accurate for computing the speed of sound, and the change in speed due to a different temperature is small enough that it can be neglected. However, if one already knows the temperature at a given altitude and wishes to calculate a more precise value for the speed of sound, the following equations can also be used. The first is specific to English units while the second applies to the Metric System. 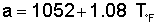 where a = speed of sound [ft/s] T°F = atmospheric temperature in degrees Fahrenheit (°F) 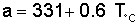 where a = speed of sound [m/s] T°C = atmospheric temperature in degrees Celsius According to these equations, a 1°F change in temperature produces a 1.08 ft/s change in the speed of sound, or a 1°C change causes a 0.6 m/s change in the speed of sound. This difference is insignificant enough that we can usually ignore it and use the standard atmospheric model as is. Values of the Speed of Sound One of the most common questions we receive is fow fast is the speed of sound, and as was pointed out earlier, there is no single value to quote. The speed of sound, also known as Mach 1, changes throughout the atmosphere based on the temperature at any given altitude. Probably the most important value to remember, however, is the speed of sound at sea level. Based on the standard atmospheric model, this value has been defined to be
If you were to reach Mach 1, or "break the sound barrier," at sea level, the above speed is how fast you would have to travel in order to do so. Another question we often receive is how fast is the speed of sound at other altitudes besides sea level. While the most accurate method of computing these values would be to use the equations listed above or an atmospheric properties calculator, we realize that this method is not always the most convenient approach. In light of this fact, we have provided tables listing the speed of sound in both English and Metric units for altitudes ranging from below sea level to the edge of the atmosphere. These tables provide the accepted values for Mach 1 in small increments of altitude allowing the reader to observe how the speed of sound varies through different regions of the atmosphere. Mach Number Examples A final question that comes up frequently is how fast is Mach 2, 3, 5, 10, or any other value besides Mach 1 at a given altitude. We first addressed this topic in a question regarding how fast is Mach 2 in miles per hour. Here, we pointed out that the Mach number is a multiple of the speed of sound. Therefore, if you know the value of Mach 1 in miles per hour, feet per second, kilometers per hour, or any other unit of measurement at the altitude in question, you merely have to multiply that value by the desired Mach number to determine the speed in that particular unit. For example, say we wanted to know the speed of a cruise missile traveling Mach 0.8 at sea level in knots. To solve the problem, we can use the speed of sound value listed above at sea level, given as 661.5 knots, and multiply it by 0.8. The answer turns out to be 529 knots. Yet another example is provided above when someone asks, "what is the speed of an aircraft traveling at Mach 3 at an altitude of 30,000 feet?" If we take another look at the Mach 1 vs. altitude tables already discussed, we see that the speed of sound at 30,000 ft is 678.2 miles per hour. All we have to do is multiply this value by 3 to determine the speed of a vehicle traveling Mach 3 at 30,000 ft in miles per hour. The answer is 2,035 mph. Let us now consider an example of the opposite problem. About 8 1/2 minutes into the flight of a Space Shuttle, the vehicle's main engines are disengaged. At that point in its trajectory, the Shuttle is traveling about 7,000 meters per second at an altitude of 110,000 m. What is the Shuttle's Mach number? If we again look at the Mach 1 vs. altitude tables, we see that the  مشكور أخى على الموضوع الجميل sonic:M=1 transonic:0.8<M<1.2 supersonic:1.2<M<5 hypersonic:M>5 وياليتك يا أخى كنت أرفقت الموضوع بالCHARTS الخاصة بالMACH NO وشكرا |
|||
|
|

|
| مشاركة [ 13 ] | ||||
|
||||
|
|
الشكر لك أخي الكريم .. الموضوع رائع ..
يعطيك العافية |
|||
|
|

|
| مشاركة [ 14 ] | |||
|
|||
|
عضو خط الطيران
|
thank you

|
||
|
|

|
| مشاركة [ 15 ] | |||
|
|||
|
عمليات المطار
|
مشكور والله يعطيك العافية
|
||
|
|

|
| مشاركة [ 16 ] | |||
|
|||
|
عضو خط الطيران
|
ألف شكر على الشرح المفصل عن سرعة الصوت
|
||
|
|

|
| مشاركة [ 17 ] | ||||
|
||||
|
|
Ranges of Speed Subsonic Usually less than Mach 0.8. Air is flowing slower than sound over every part of the airplane. Transonic About Mach 0.8 to Mach 1.2. Air is flowing faster than sound over some parts of the airplane. Supersonic Greater than about Mach 1.2. Air is flowing faster than sound over the entire airplane. Hypersonic Greater than about Mach 5. Heat becomes a critical factor.
|
|||
|
|

|
| مشاركة [ 18 ] | ||||
|
||||
|
|
What Is a Mach Number
The speed of sound depends on temperature--and therefore altitude. We use Mach numbers to describe an airplane's speed in terms of the speed of sound. An airplane moving at Mach 1 is traveling at the speed of sound. Mach 0.5 is half the speed of sound, Mach 2 is twice the speed of sound, and so on. |
|||
|
|

|
| مشاركة [ 19 ] | ||||
|
||||
|
|
Thank you too much
|
|||
|
|

|